快速排序是一种常用的排序算法,其核心思想是通过将数组分割成较小的子数组来逐步完成排序。本文将详细介绍分割数快速排序的原理和应用场景,并通过15个的内容逐步教你掌握这一算法。
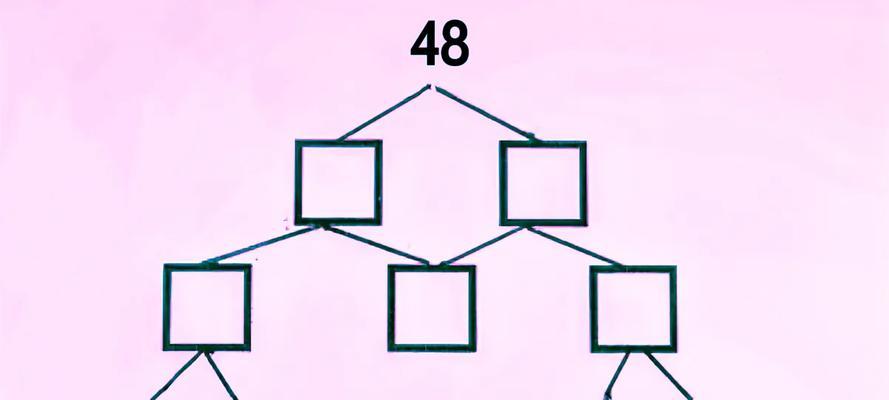
什么是分割数快速排序
分割数快速排序是一种基于快速排序算法的优化版本,在每次递归时选择一个特定的数作为分割点,将数组分割为两部分,并对这两部分进行排序。
分割数的选择
在分割数快速排序中,选择合适的分割数对算法的效率有着重要的影响。一般来说,可以选择数组的中间元素作为分割数,也可以通过其他方法选择。
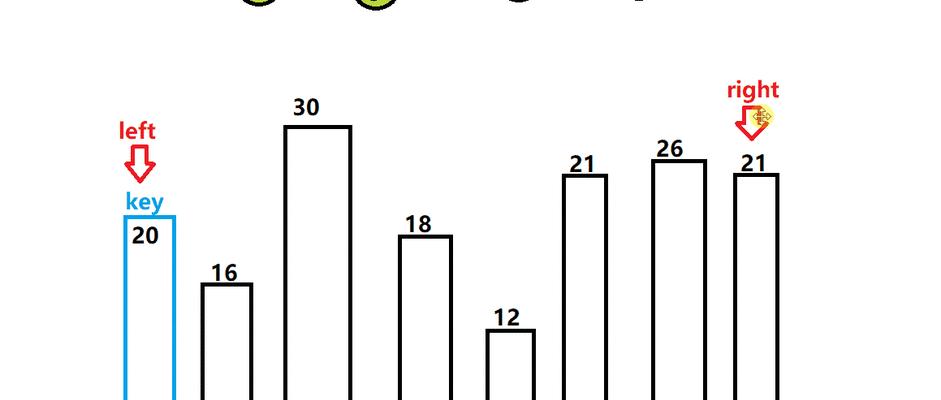
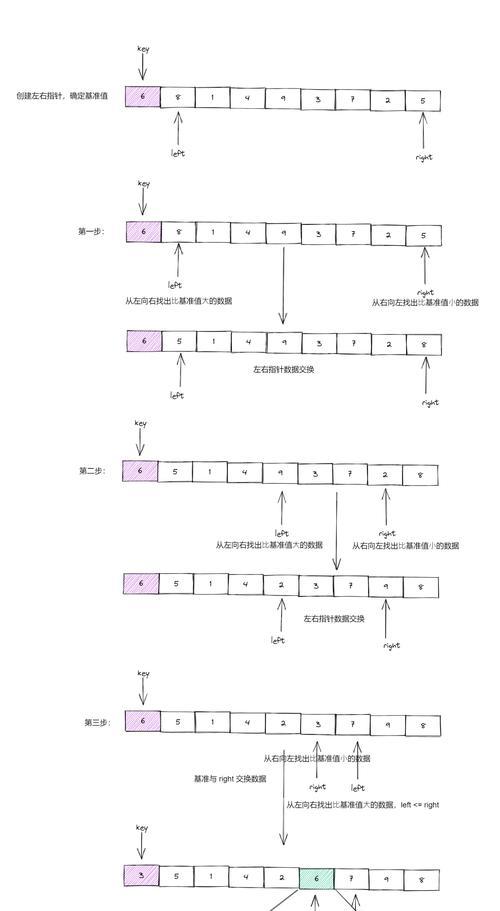
分割过程详解
通过选择好的分割数,将数组划分为两个子数组,其中左边子数组中的元素都小于等于分割数,右边子数组中的元素都大于等于分割数。
递归调用
在分割过程完成后,对左边和右边的子数组分别进行递归调用,继续进行分割数快速排序。
时间复杂度分析
分割数快速排序的平均时间复杂度为O(nlogn),其中n为数组的长度。这使得它成为一种高效的排序算法。
空间复杂度分析
分割数快速排序的空间复杂度为O(logn),主要消耗在递归调用时的栈空间。
稳定性分析
分割数快速排序是一种不稳定的排序算法,即可能改变相同元素的相对顺序。
应用场景1-大数据排序
分割数快速排序在大数据排序中表现出色,能够高效地处理海量数据。
应用场景2-查找问题
分割数快速排序也可以用于解决一些查找问题,例如寻找数组中的第k大元素。
优化思路1-三数取中法
为了选择更好的分割数,可以采用三数取中法,即选择数组的首、中、尾元素中的中位数作为分割数。
优化思路2-随机选择分割数
随机选择分割数可以降低最坏情况出现的概率,提高算法的鲁棒性。
优化思路3-插入排序
当待排序的子数组长度较小时,可以切换到插入排序等其他简单排序算法,以减少递归调用的开销。
应对重复元素
在处理存在大量重复元素的情况下,可以采用双路快速排序或三路快速排序等变体算法来提高效率。
算法实现注意事项
在实现分割数快速排序时,需要注意边界条件、数组越界等细节问题,以保证算法的正确性。
分割数快速排序是一种高效的排序算法,具有广泛的应用场景。通过选择合适的分割数和优化思路,可以进一步提升算法的性能。熟练掌握这一算法对于编程人员来说是必不可少的技能。


